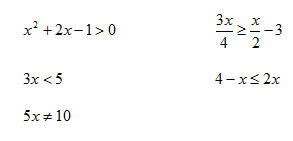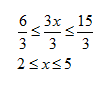Solving
| Site: | Harrison |
| Course: | Michigan Algebra I Sept. 2012 |
| Book: | Solving |
| Printed by: | Guest user |
| Date: | Saturday, 20 December 2025, 8:35 AM |
Description
Introduction
An expression that contains the symbol >, <, > or < is called an inequality. An inequality expresses the relative order of two mathematical expressions. The expressions can be either numerical or variable expressions.
An inequality is written using the following symbols.

Examples of inequalities include:
Addition & Subtraction
In solving an inequality, the goal is to write the variable on one side of the inequality symbol and a constant on the other side. The Addition Property of Inequality states that the same number can be added to both sides of an inequality without changing the solution set.
Addition Property of Inequality
If a > b, then a + c > b + c, andif a < b, then a + -c < b + -c
Using this property in solving inequalities is a lot like solving linear equations.
Examples
Example 1 Solve x + 3 < 0.
Treat this problem like an equation and subtract 3 from both sides of the inequality.
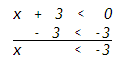
x < -3
Example 2 Solve x + 5 > 3.
Treat this problem like an equation and subtract 5 from both sides of the inequality.
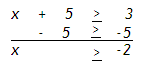
x ? -2
Video Lesson
To see more examples on solving linear inequalities, select the following links:
Multiplication & Division
The process continues to be similar to solving linear equations, except for one main difference, that occurs when multiplying or dividing by a negative number. The Multiplication Property of Inequalities states that the same positive number can be multiplied to both sides of an inequality without changing the solution set. If the same negative number is multiplied on both sides of the inequality the sign must be reversed. Consider 3 > 2. What happens to the inequality when both sides are multiplied by -1? The temptation is to say that the answer will be "-3 > -2". But -3 is not greater than -2; it is indeed smaller. The correct inequality is -3 < -2.
If a > b andc > 0, then ac > bc; and if a < b and c > 0, then ac < bc.
Or
If a>b andc < 0, then ac<bc; and if a<b andc < 0, then ac>bc.
Examples:
7 > 2 7?-4 > 2?-4 -28 < -8
Examples
Example 1 Solve 2x< 9.
Divide both sides by 2. Since 2 > 0 the sign will remain the same.

Example 2 Solve ![]() .
.
Multiply both sides by 4. Since 4 > 0 the sign will remain the same.
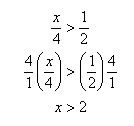
Example 3 Solve -2x < 5.
Divide both sides of the inequality by - 2, remember to reverse the inequality symbol.
-2x < 5
-2x > 5
-2 -2
x > - ![]()
Video Lesson
To see more examples on solving linear inequalities, select the following links:
Multi-Step
The process for solving multi-step inequalities is exactly the same as solving multi-step equations. The only difference is when there is a multiplication or division by a negative number, the inequality symbol will switch directions.
Example 1 Solve ![]() .
.
Step 1. Multiply both sides of the inequality by 4.
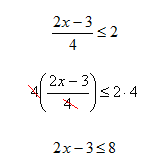
Step 2. Add three to both sides of the inequality.
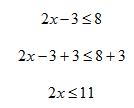
Step 3. Divide both sides by 2. Since 2 > 0, there is no symbol change.

Example 2
Solve 5x + 7 < 3(x + 1).
5x + 7 < 3(x + 1)
5x + 7 < 3x + 3
Step 2. Subtract 3x from both sides.

Step 3. Subtract 7 from both sides.
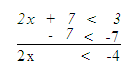
Step 4. Divide both sides by 2, since 2 > 0 there is no symbol change.

Example 3
Solve 3(x - 2) + 4 > 2(2x - 3).

Step 2. Subtract 3x from both sides.

Step 3. Add 6 to both sides.
Compound Inequalities
A compound inequality has more than one inequality sign. Solving a compound inequality is similar to solving regular inequalities, except that it has three or more "parts". So, when a number is added, subtracted, multiplied or divided it is done to all of the parts separated by the inequality symbols.
Example Solve 10 < 3x + 4 < 19.
Step 1. Subtract 4 from all "parts".

Step 2. Divide all sides by 3. Since 3 > 0, there is no symbol change.
Practice
Solving Inequalities Worksheet
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Answer Key
Solving Inequalities Answer Key
*Note: If Google Docs displays "Sorry, we were unable to retrieve the document for viewing," refresh your browser.
Sources
Holt, Rinehart, & Winston. "Systems of Equations and Inequalities." http://my.hrw.com/math06_07/nsmedia/homework_help/alg1/
alg1_ch06_05_homeworkhelp.html (accessed August, 5, 2010)
Stapel, Elizabeth. "Solving Linear Inequalities: Advanced Examples." Purplemath. Available from http://www.purplemath.com/modules/
ineqlin3.htm. Accessed 15 August 2010