Characteristics
| Site: | Harrison |
| Course: | Michigan Algebra I Sept. 2012 |
| Book: | Characteristics |
| Printed by: | Guest user |
| Date: | Wednesday, 24 December 2025, 12:49 PM |
Description
A function is considered to be a quadratic function if the equation has a degree or highest exponent of 2. The standard form of a quadratic equation is y = ax2 + bx + c where a, b, c are real numbers and a![]() 0. All functions of this form have similar characteristics.
0. All functions of this form have similar characteristics.
Introduction
Graphs of Quadratics
The graph of any quadratic function has a "U" shape and is called a parabola. Parabolas always have a line of symmetry that passes through the parabola's vertex. In all parabolas that are considered to be functions, this line of symmetry will be vertical and have an equation in the form x = h, where h is the x-coordinate of the vertex.
The specific values of a, b, and c control where the curve is relative to the origin (left, right, up, or down), and how rapidly it spreads out. Also, if the value of a is negative then the parabola will be reflected across the x-axis before it is translated left, right, up or down.
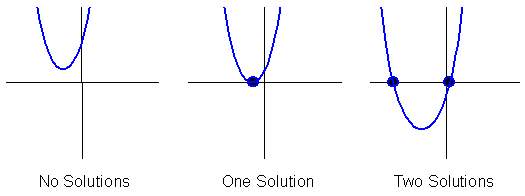
All quadratic functions have one y-intercept and two, one or no x-intercepts. The x-intercepts of the graph are the same as the solutions of the corresponding quadratic equation. Solutions to quadratic equations can also be called roots. Quadratic equations can have two, one, or no real roots. The figures below demonstrate the different solution sets of a quadratic equation.
Tables of Quadratics
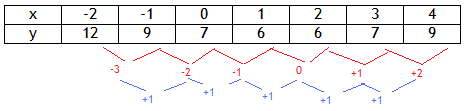
In table form, all quadratic functions have a common second difference. This can be useful not only in identifying if a certain set of data can be modeled by a quadratic function, but also in determining what quadratic function would model the data. The table below demonstrates a set of data that can be modeled by a quadratic function. Since the x-coordinates are going up by one every time, the constant second difference of the y -coordinates means this table can be modeled by a quadratic function.
Video Lesson
To learn more about basic characteristics of quadratics, please select the following link:
Sources
Embracing Mathematics, Assessment & Technology in High Schools; A Michigan Mathematics & Science Partnership Grant Project
Holt, Rinehart & Winston, "Characteristics of Quadratic Functions." http://my.hrw.com/math06_07/nsmedia/lesson_videos/alg1/player.html?contentSrc=6371/6371.xml (accessed 8/18/210).
Walsh, Shelley. "Shelley's Mathematical Articles." http://homepage.mac.com/ shelleywalsh/MathArt/mathart.htm (accessed 7/13/2010).