Print bookPrint book

Factoring

Site: Harrison
Course: Michigan Algebra I Sept. 2012
Book: Factoring
Printed by: Guest user
Date: Thursday, 21 November 2024, 3:04 PM

Description

Factoring

Table of contents

Introduction

Factoring a quadratic equation is sometimes the easiest way to find the solutions. However, not all quadratics are factorable. It is always a good idea to check if this method works before moving on to other methods of solving. If the value of a is not 1, it is often easier to use the quadratic formula rather than factoring.


Zero Product Property

A quadratic equation is in factored form when it is rewritten as the product of two linear expressions. In general, the factored form of a quadratic is written as y = (x - R1) (x- R2) where R is equal to the roots of the equation. The Zero Product Property is then used to determine the solutions.

The Zero Product Property states if ZeroProduct , then either a = 0 or b = 0. This is particularly useful when solving quadratic equations.

Example Solve the equation (x + 5)(x - 4) = 0.

Step 1. Use the Zero Product Property to set up two equations.

Since (x + 5)(x - 4) = 0, either x + 5 = 0 or x - 4 = 0.

Step 2. Solve each equation.

x = -5 or x = 4

*Note: x = -5 or 4 are the roots of the equation and the x -intercepts of the graph.


Factoring

The simplest case for factoring is when a = 1. In order to factor a quadratic of the form x2 + bx + c , find two numbers whose product is the value of c and whose sum is the value of b . Start by finding all the factors of c. Then determine which of these factor pairs adds up to b . This factor pair will be the roots that are substituted in to the factored form. Finally, to find the solutions, use the Zero Product Property to set each factor equal to zero and solve.


Example 1

Factor and solve x2 + 7x + 6 = 0

Step 1. List all factor pairs of c.

In this equation c = 6. The factor pairs of 6 are 1 and 6, 2 and 3.

Step 2. Determine which factor pair has a sum of b.

In this equation b = 7.
The sum of the factor pairs are 1 + 6 = 7 and 2 + 3 = 5.
1 and 6 have the correct sum.

Step 3. Substitute the roots into the factored form.

(x + 1)(x + 6) = 0

Step 4. Use the Zero Product Property to set each factor equal to zero and solve.

x + 1 = 0 or x + 6 = 0

x = -1 or x = -6

*Note: The Commutative Property of Multiplication says that order does not matter in multiplication, so the factored form could also be written ( x + 6)( x + 1).

Example 2

Factor and solve x2 - 2x - 8 = 0.

Step 1. List all factor pairs of c.

In this equation c = -8.
The factor pairs of -8 are 1 and -8, -1 and 8, -2 and 4, 2 and -4.


Step 2. Determine which factor pair has a sum of b.

In this equation b = -2.
The sum of the factor pairs are -8 + 1 = -7, -1 + 8 = 7, -2 + 4 = 2, and 2 + -4 = -2.

2 and -4 have the correct sum.


Step 3. Substitute the roots into the factored form.

(x + 2)(x - 4) = 0


Step 4. Use the Zero Product Property to set each factor equal to zero and solve.

x + 2 = 0 or x - 4 = 0

x = -2 or x = 4


Signs

As noted in previous examples, the signs on b and c give clues to determine which factors to use.

  • If c is positive, then the factors must have the same sign.
    • If b is positive, then the factors are positive.
    • If b is negative, then the factors are negative.
  • If c is negative, then the factors must have opposite signs; that is, one is negative and one is positive.
    • If b is positive, then the larger factor is positive.
    • If b is negative, then the larger factor is negative.


When a is not 1

If a is not equal to 1, first check to see if a common factor can be factored out of the equation. For example, in y = 2x2 + 8x + 8 notice that a, b, and c are all even numbers and therefore all have a factor of 2. The factor of two can be divided out before factoring the remaining equation. After factoring out the two, the equation becomes y = 2(x2 + 4x +4). Now the equation that remains has an a-value of 1 and can be factored like the previous two examples.

If there is not a factor common to all the terms, all three coefficients must be used to determine the factors. First multiply a and c , then find the factor pair of ac that has a sum of b . Substitute this factor pair into the original equation in place of the b and then factor by grouping the first two terms and the last two terms and determining the GCF of each.


Example 1

Factor and solve 2x2 + x - 6 = 0.

Step 1. Multiply a and c.

In this equation, a = 2 and c = -6, therefore ac = -12.

Step 2. List all factor pairs of ac.

In this equation ac = -12.
The factor pairs of -12 are 1 and -12, -1 and 12, 2 and -6, -2 and 6, 3 and -4, -3 and 4.

Step 3. Determine which factor pair has the sum of b.

In this equation b = 1.
The sum of the factor pairs are 1 + -12 = -11, -1 + 12 = 11, 2 + -6 = -4, -2 + 6 = 4, 3 + -4 = -1, -3 + 4 = 1.

4 and -3 have the correct sum.

Step 4. Substitute the roots into the original equation in place of b.

2x2 + (4 + -3)x - 6 = 0

2x2 + 4x + -3x - 6 = 0

Step 5. Factor by grouping the first two terms and the last two terms together and find their GCF.

(2x2 + 4x) + (-3x - 6) = 0

2x(x + 2) -3(x + 2) = 0

(x + 2)(2x - 3) = 0

Step 6. Use the Zero Product Property to set each factor equal to zero and solve.

x + 2 = 0 or 2x - 3 = 0

x = -2 or x = 1.5

Area Model Method

After finding the factor pair that has a product of ac and a sum of b, it is possible to use an area model to help factor the four terms.

Example Factor and solve 2x2 + x - 6 = 0 (same equation from last example).

After following steps 1 - 3 in the previous example, the factor pair needed is -3 and 4. At this point the rest of the steps will be based on the area model.

Step 4. Enter the first and last terms into the area model in the upper left and lower right squares.

AreaModel1

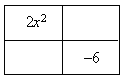
Step 5. Enter the factor pair determined earlier into the other two squares. Because of the Commutative Property of Multiplication, it does not matter which factor is put in which square.

AreaModel2

Step 6. Factor the GCF from each row and column and write them on the outside of the box.

AreaModel3

Step 7. The two terms across the top create one binomial and the two terms along the left-hand side create the other binomial. The factored form is:

(2x - 3)(x + 2) = 0

Step 8. Use the Zero Product Property to set each factor equal to zero and solve.

2x - 3 = 0 or x + 2 = 0

x = 1.5 or x = -2


Perfect Square Trinomials

Sometimes the trinomial that needs to be factored is a perfect square trinomial. A perfect square trinomial is a trinomial that can be written so that its first term is the square of some quantity a, its last term is the square of some quantity b, and its middle term is twice the product of the quantities a and b. There are special formulas that can be used to factor these perfect square trinomials:

a2 + 2ab + b2 = (a + b)2

a2 - 2ab + b2 = (a - b)2

Example 1 Factor x2 + 10x + 25

Step 1. Determine if the first and last terms are perfect squares.

The first term is x2, which is (x)2 - yes.

The last term is 25, which is (5)2 - yes.

Step 2. Determine if the middle term fits the pattern 2ab.

a = 1 and b = 5

The middle term is 10x, which is 2 (5)(1)x - yes.

Step 3. Substitute values for a and b into the formula.

x2 + 10 x + 25 = (1x) 2 + 10x + (5) 2 = (x + 5) 2 .

.

Example 2

Factor 16x2 + 24xy + 9y2

Step 1. Determine if the first and last terms are perfect squares.

The first term is 16x2, which is (4x)2 - yes.

The last term is 9y2, which is (3y)2 - yes.

Step 2. Determine if the middle term fits the pattern 2ab.

a = 4 and b = 3

The middle term is 24xy, which is 2(4)(3)xy - yes.

Step 3. Substitute values for a and b into the formula.

16x2 + 24xy + 9y 2 = (42)x2 + (2)(4)(3)xy + (32)y2 = (4x + 3y)2 .



Difference of Two Squares

There are binomials that can be more easily factored if the pattern is recognized. One of these binomials is the difference of squares:

a2 - b2 = (a + b)(a - b)

Notice that there is no middle term in the binomial. When (a + b) and (a - b) are multiplied the new expression is a2 + ab - ab - b2, since the two middle terms cancel the remaining expression is a2 - b2. This pattern only works when the two terms are subtracted.

Example 1 Factor x2 -16

Step 1. Determine if the first and last terms are perfect squares.

The first term is 1x2, which is (1x)2 - yes.

The last term is 16, which is (4)2 - yes.

Step 2. Since the two terms are also being subtracted, substitute values for a and b into the Difference of Squares formula.

x2 - 16 = (1x)2 - (4)2 = (x + 4)(x - 4)

Example 2 Factor 9x2 - 4y2

Step 1. Determine if the first and last terms are perfect squares.

The first term is 9x2, which is (3x)2 - yes.

The last term is 4y2, which is (2y)2 - yes.

Step 2. Since the two terms are also being subtracted, substitute values for a and b into the formula.

9x2 - 4y2 = (3x + 2y)(3x - 2y)

Video Lesson

To learn how to solve quadratics by factoring, select the following link:

Solve Quadratics by Factoring

Interactive Activities

To see how to factor quadratic trinomials, select the following link:

Factoring Trinomials #1

Factoring Trinomials #2

Guided Practice

To solidify your understanding of complex numbers, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.

Guided Practice

Practice

Solve by Factoring Worksheet

More Factoring Worksheet

*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Answer Keys

Solve by Factoring Answer Key

More Factoring Answer Key

*Note: If Google Docs displays “Sorry, we were unable to retrieve the document for viewing,” refresh your browser.

Sources

Embracing Mathematics, Assessment & Technology in High Schools; A Michigan Mathematics & Science Partnership Grant Project

"Factoring Quadratics." http://distance-ed.math.tamu.edu/peic/applets/quadratic_solver.htm (accessed 08/07/2010).

Holt, Rinehart & Winston, "Quadratic Equations and Functions." http://my.hrw.com/math06_07/nsmedia/homework_help/alg1/alg1_ch09_06_homeworkhelp.html (accessed 7/22/2010).

Hot Math, "Zero Product Property." http://hotmath.com/hotmath_help/topics/zero-product-property.html (accessed 07/22/2010).

MathisFun, "Factoring Quadratics." http://www.mathsisfun.com/algebra/factoring-quadratics.html (accessed 07/22/2010).

Peterson, Roy. "Factoring Polynomials." http://www.wisc-online.com/objects/ViewObject.aspx?ID=TMH1702 (accessed 7/22/2010).

Purple Math, "Factoring Quadratics: The Hard Case." http://www.purplemath.com/modules/factquad.htm (accessed 07/22/2010).

Purple Math, "Factoring Quadratics: The Simple Case." http://www.purplemath.com/modules/factquad.htm (accessed 07/22/2010).

University of Wisconsin, "Solving Quadratic Trinomials." http://www.wisc-online.com/objects/ViewObject.aspx?ID=TMH1702 (accessed 07/16/2010).