Graphs
| Site: | Harrison |
| Course: | Michigan Algebra I Sept. 2012 |
| Book: | Graphs |
| Printed by: | Guest user |
| Date: | Thursday, 21 November 2024, 4:48 PM |
Description
Graphs
From A Graph
Example 1 Determine the function that models the graph below:
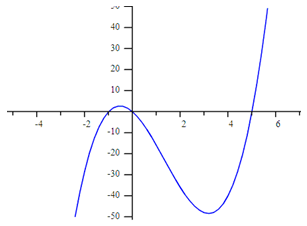
Step 1. Determine the zeros of the function.
(-1, 0), (0, 0), (5, 0)
Step 2. Turn each zero into a factor of the function.
Since x = -1, then (x + 1) is a factor of the polynomial.
Since x = 0, then (x) is a factor of the polynomial.
Since x = 5, then ( x - 5) is a factor of the polynomial.
Example 1 Continued
y = a (x + 1)(x)(x - 5); point (4, -40)
-40 = a (4 + 1)(4)(4 - 5)
-40 = a (5)(4)(-1)
-40 = a (-20)
2 = a
Example 2
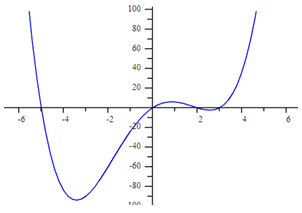
Step 1. Determine the zeros of the function.
(-5, 0), (0, 0), (2, 0), (3, 0)
Step 2. Turn each zero into a factor of the function.
Since x = -5, then (x + 5) is a factor of the polynomial.
Since x = 0, then (x) is a factor of the polynomial.
Since x = 2, then (x - 2) is a factor of the polynomial.
Since x = 3, then (x - 3) is a factor of the polynomial.
Step 3. Determine the factored form of the polynomial by using another point from the graph. Substitute the point in for (x, y) and solve for the value of a.
y = a (x + 5)(x)(x - 2)(x - 3); point (-2, -60)
-60 = a (-2 + 5)(-2)(-2 - 2)(-2 - 3)
-60 = a (3)(-2)(-4)(-5)
-60 = a (-120)
.5 = a
Practice
Answer Key
Source
Embracing Mathematics, Assessment & Technology in High Schools; A Michigan Mathematics & Science Partnership Grant Project