Inverses
| Site: | Harrison |
| Course: | Michigan Algebra I Sept. 2012 |
| Book: | Inverses |
| Printed by: | Guest user |
| Date: | Saturday, 31 January 2026, 4:07 AM |
Description
Graphs
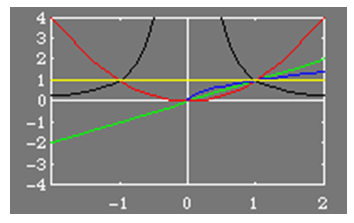
Recall from the previous lesson, that the family of functions known as the power functions take the form, y = kxp. The shape of the graph of these power functions depends on the sign of k and the value of p. The coefficient k will change the scale of the graph and, if negative, flip the graph across the x-axis.
All graphs of y = xp pass through the point (1,1). Beyond that, the shape and growth for large positive x is given by:
· p >1: resembles a quadratic when even or a cubic when odd. Grows as x grows larger. Example: y = x2
· p = 1: the line y = x. Grows as x grows larger. Example: y = x
· 0 < p <1: concave down. Grows as x grows larger. Example: y = x(½)
· p = 0: the line y = 1. Example:y = x0 = 1
Finding Inverses
Recall from earlier lessons, that inverse graphs are reflections across the line y = x. To find the inverse of a power function, switch the x and y and solve for y. To graph the inverse of a power function, switch the x and y-coordinates of the points and plot the results.
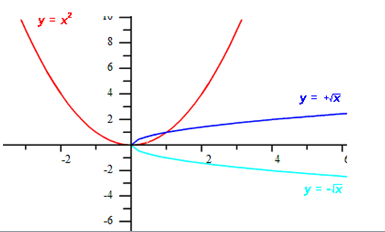
Example Find the inverse of the function: y = x2 , then graph both equations.
Step 1. Switch the x and the y.
x = y2
Step 2. Solve for y.
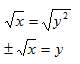
The inverse of ![]() is
is ![]()
Step 3. Graph the equations.
Direct & Inverse Relationships
To see where this relationship comes from, find the inverse of y = kx.
x = ky
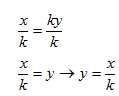
The inverse of y = kx is ![]() .
.
Video Lessons
To learn more about the direct and inverse relationships of a function select the following links:
Identifying Inverse Variation Video
Guided Practice
To solidify your understanding inverse functions, visit the following link to Holt, Rinehart and Winston Homework Help Online. It provides examples, video tutorials and interactive practice with answers available. The Practice and Problem Solving section has two parts. The first part offers practice with a complete video explanation for the type of problem with just a click of the video icon. The second part offers practice with the solution for each problem only a click of the light bulb away.
Sources
Bogley, William A & Robson, Robby. "Power Functions." http://oregonstate.edu/instruct/mth251/cq/FieldGuide/power/lesson.html (accessed September 3, 2010).
Holt, Rinehart, & Winston. "Exponential & Logarithmic Functions." http://my.hrw.com/math06_07/nsmedia/homework_help/alg2/
alg2_ch07_02_homeworkhelp.html (accessed September 12, 2010).
Holt, Rinehart, & Winston. "Polynomial Function." http://my.hrw.com/math06_07/nsmedia/homework_help/alg2/
alg2_ch06_07_homeworkhelp.html (accessed September 3, 2010).
Stapel, Elizabeth. "Symmetry and Graphing." Purplemath. Available from http://www.purplemath.com/modules/symmetry3.htm. Accessed 12 September 2010
Stapel, Elizabeth. "Variation Equations." Purplemath. Available from http://www.purplemath.com/modules/variatn2.htm. Accessed 12 September 2010